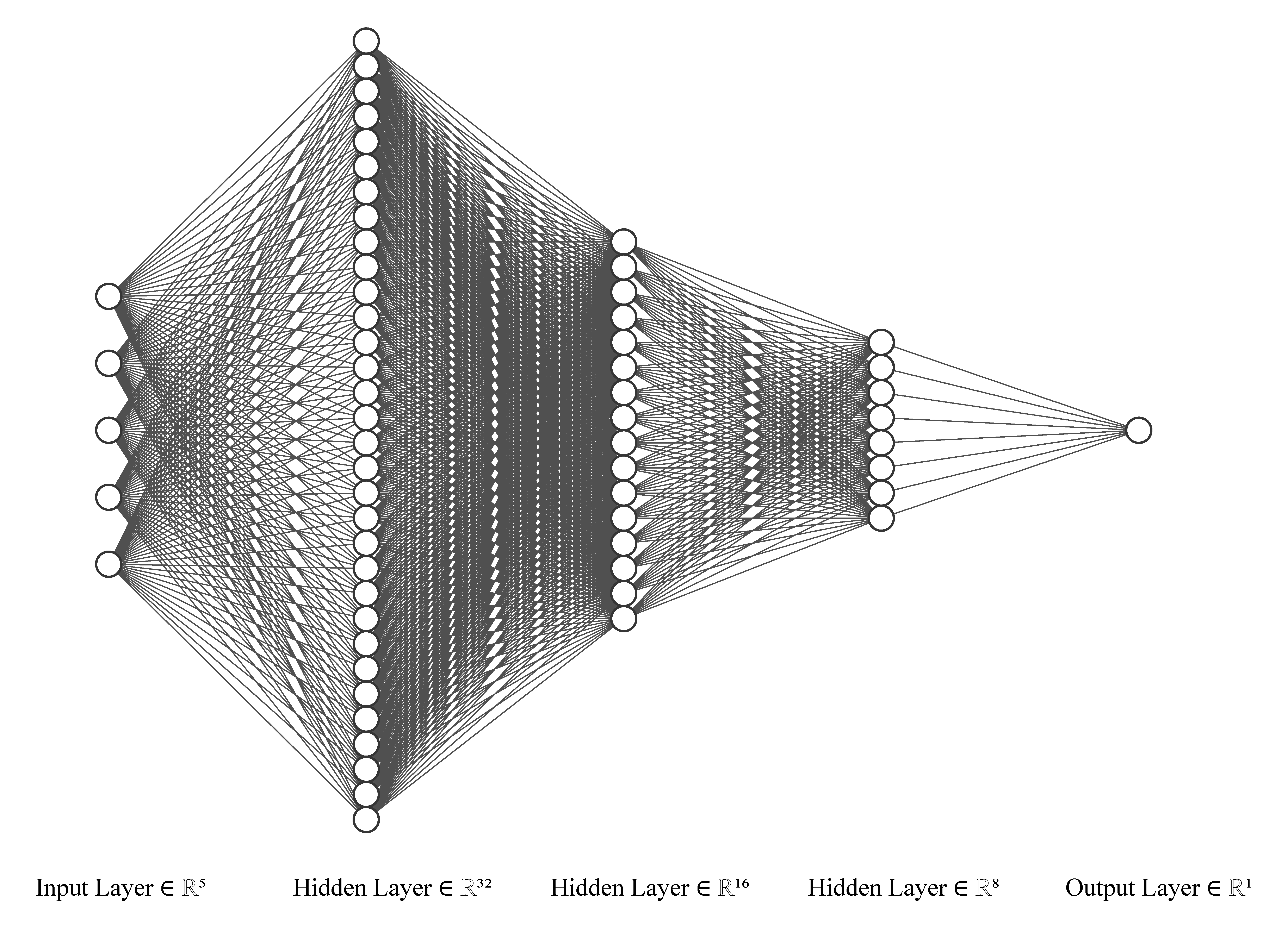
Geometric Pyramid Rule #

The architecture of a neural network is determined by not only its depth but also the number of units in each layer. The example earlier (link here) uses an architecture with depth $D=3$, and number of hidden units $M_1=3$ and $M_2=4$ in the first and second hidden layer respectively. These choices are somewhat arbitrary.

A more systematic approach proposed in Masters (1993) is the geometric pyramid rule, which keeps reducing the number of hidden units by half when adding a new layer. The following figure illustrates this idea with $M_1=2^{5}=32$, $M_2=2^{4}=16$ and $M_3=2^3=8$.

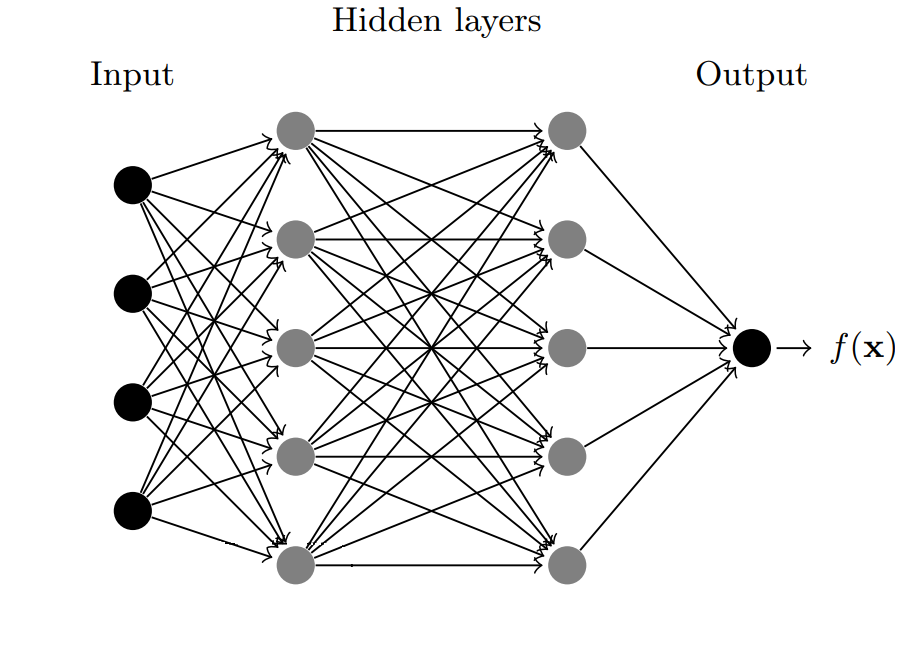
Fully-Connected Networks #

The geometric pyramid rule can be useful but it is not convenient for very deep neural networks. If we fix the number of the units in the last hidden layer, the number of totally units grow exponentially with depth and this may create both computational and statistical problems.

When the depth $D$ is relatively large, a more common approach is to simply fix the same number of units $M_1=M_2=\ldots=M_{D-1}=M$ across all hidden layers, and $M$ is the width of the network. This approach gives the fully-connected network, or multilayer perceptron (MLP). The total number of hidden units for a MLP equals $M(D-1)$ which grows only linearly in depth $D$ for a given width $M$. The figure below illustrates the architecture with depth $D=3$ and width $M=5$.