Universal Approximation Theorem #

The XOR function is merely an example showing the limitation of linear models. In real-life problems, we do not know the true regression function, which can be (highly) nonlinear in many situations. The collection of neural networks forms a systematic model thanks to their universal approximation property.

For any sufficiently smooth function $\mu$ on a compact set with finitely many discontinuities, there exists a feedforward network $f$ that can approximate it arbitrarily well if:

• the number of hidden units $M$ is sufficiently large;
• the activation function $\sigma$ is not polynomial.

The precise smoothness conditions on $\mu$ are rather technical and omitted.

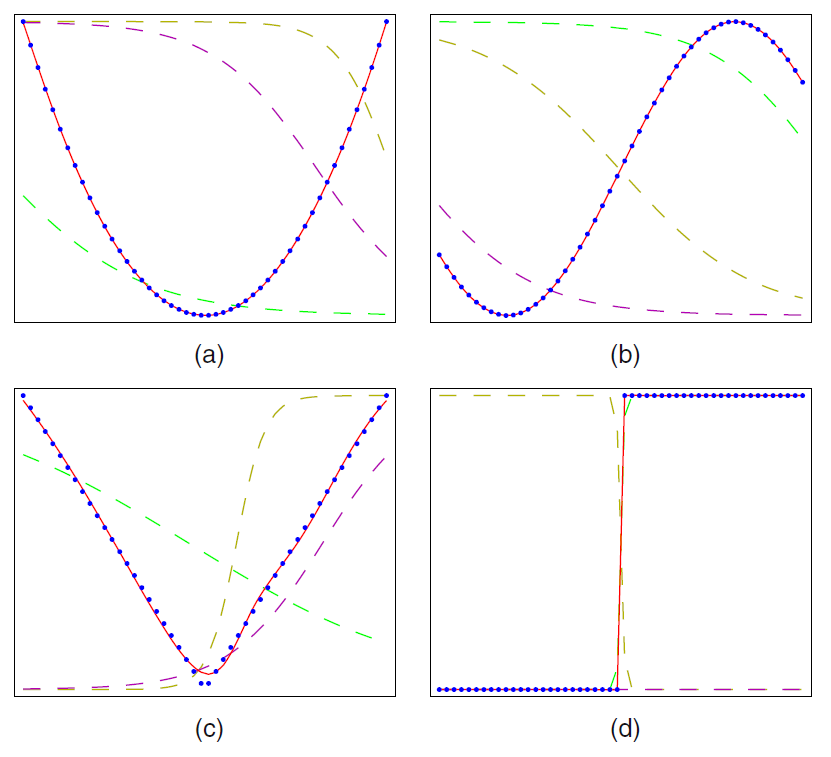
If $\mu$ has a derivative $\mu'$, then there exists a shallow neural network $f$ such that $(f,f')$ approximates $(\mu,\mu')$ arbitrarily well simulatenously under similar conditions. The following figure from Bishop (2006) illusrates the excellent approximation performance of the shallow neural networks against four example univariate regression functions:

(a) $\mu(x)=x^2$

(b) $\mu(x)=\sin(x)$

(c) $\mu(x)=|x|$

(d) $\mu(x)=\mathbf{1}[x>0]$

The dots are on the true regression functions, the dashed lines are the outputs of hidden units, and the solid line shows the approximation by a single-output shallow neural network.

How Useful Is Universal Approximation Theorem? #

The universal approximation property, however, does not tell precisely how many hidden units are required. Some literature does provide upper bounds for the required number of hidden units given a certain amount of approximation error. However, these upper bounds are usually too large to be practical. Improving these bounds is challenging and remains an active research area. The actual implementation still relies on domain knowledge. Filling this gap between theory and practice is one of the most exciting research areas in machine learning.