Bayes Classifier VS Regression Function #

Consider the two-class classification problem with a label set given by $\mathcal{Y}=\{-1,1\}$, without loss of generality. The regression function for the binary variable $Y$ is given by $$\begin{align*} \mu(x)=&\mathbb{E}[Y\mid X=x]\\=&\mathbb{P}(Y=1\mid X=x)\cdot 1\\&+\mathbb{P}(Y=-1\mid X=x)\cdot (-1)\\=&\mathbb{P}(Y=1\mid X=x)\\&-\mathbb{P}(Y=-1\mid X=x).\end{align*} $$

The Bayes classifier becomes nothing else but the sign of the regression function

$$ \underset{y\in\{-1,1\}}{\operatorname{argmax}}~\mathbb{P}(Y=y\mid X=x) =\operatorname{sign}(\mu(x)) $$

except for the feature values at the decision boundary $\{x:\mu(x)=0\}$ for which we can arbitrarily assign the labels.

Multiple-Class Classification #

What if we have multiple labels, say, with $\mathcal{Y}=\{\mathcal{C}_1,\ldots,\mathcal{C}_K\}$ for some finite $K\geq 2$? Unfortunately, the sign trick above is insufficient to distinguish more than two classes. To handle more classes, we need to encode the categorical target using a vector of dummy variables.

One-Hot Encoding #

The one-hot encoding of categorical target $Y\in \{\mathcal{C}_1,\ldots,\mathcal{C}_K\}$ is the vector given by $$(Y^{(1)},\ldots,Y^{(K)})\in \{0,1\}^K$$ with $$Y^{(k)}=\mathbf{1}[Y=\mathcal{C}_k],~1\leq k\leq K$$ where $\mathbf{1}[A]$ denotes the indicator function that equals to 1 if condition $A$ is satisfied and equals to 0 otherwise.

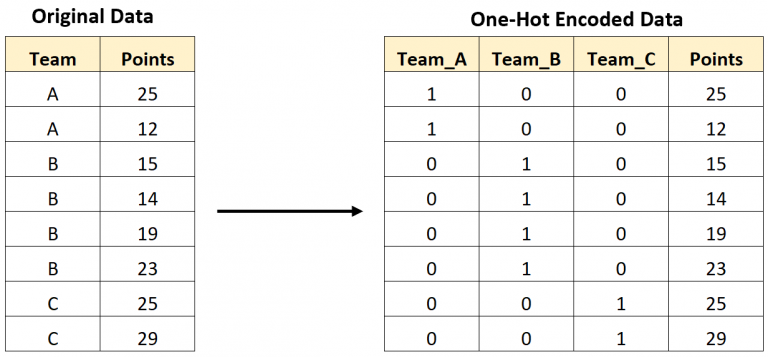
In this example, there are $K=3$ teams with labels A, B, and C. We convert each observation of the label A/B/C into a vector of 3 dummies.

The $K$-dimensional regression function for the one-hot encoded target is given by

$$\mu(x)=(\mu_1(x),\ldots,\mu_K(x))$$ where $$\begin{align*}\mu_k(x)=&\mathbb{E}[Y^{(k)}\mid X=x]\\=&\mathbb{P}\left( Y=\mathcal{C}_k\mid X=x\right).\end{align*}$$

With one-hot encoding, one can now estimate the Bayes classifier using a two-step procedure:

• First estimate the multivariate regression function $\mu(x)$
• Then choose the label $h(x)\in\{\mathcal{C}_1,\ldots,\mathcal{C}_K\}$ with largest regression value.