Consider a classification problem with $K$ labels and the one-hot encoded target $(Y^{(1)},\ldots,Y^{(K)}) \in\{0,1\}^K$. Fitting a candidate prediction rule, say, $f_k(x)$ separately to each regression function $\mathbb{P}[Y^{(k)}=1|X=x]$ may violate the axioms of probability.

Axioms of Probability #

For all $x\in\mathcal{X}$: $$f_{1}(x),\ldots,f_{K}(x)\geq 0,\\ \sum_{k=1}^{K} f_{k}(x)=1.$$

Relaxing this condition complicates our estimators’ interpretation and worsens our predictions’ statistical performance. One way to impose the axioms is to model the posterior probabilities jointly by

$$\begin{pmatrix}f_{1}(x)\\\vdots\\f_{K}(x)\end{pmatrix}=\boldsymbol{\sigma}\begin{pmatrix}a_{1}(x)\\\vdots\\a_{K}(x)\end{pmatrix}=\boldsymbol{\sigma}(a(x)) ,$$ where $\boldsymbol{\sigma}:\mathbb{R}^{K}\rightarrow\mathbb{R}^K$ is the softmax function mapping real-valued functions $a_{k}$ to posterior probabilities:

Softmax Function #

The softmax function $\boldsymbol{\sigma}:\mathbb{R}^K\rightarrow [0,1]^K$ is defined as follows: for all $a=(a_1,\ldots,a_K)^T\in\mathbb{R}^K$

$$\boldsymbol{\sigma}(a)=\begin{pmatrix}\boldsymbol{\sigma}(a)_1\\\vdots\\\boldsymbol{\sigma}(a)_K\end{pmatrix},$$ with $$\boldsymbol{\sigma}(a)_k=\frac{\exp(a_k)}{\sum_{j=1}^{K}\exp(a_{j})}.$$

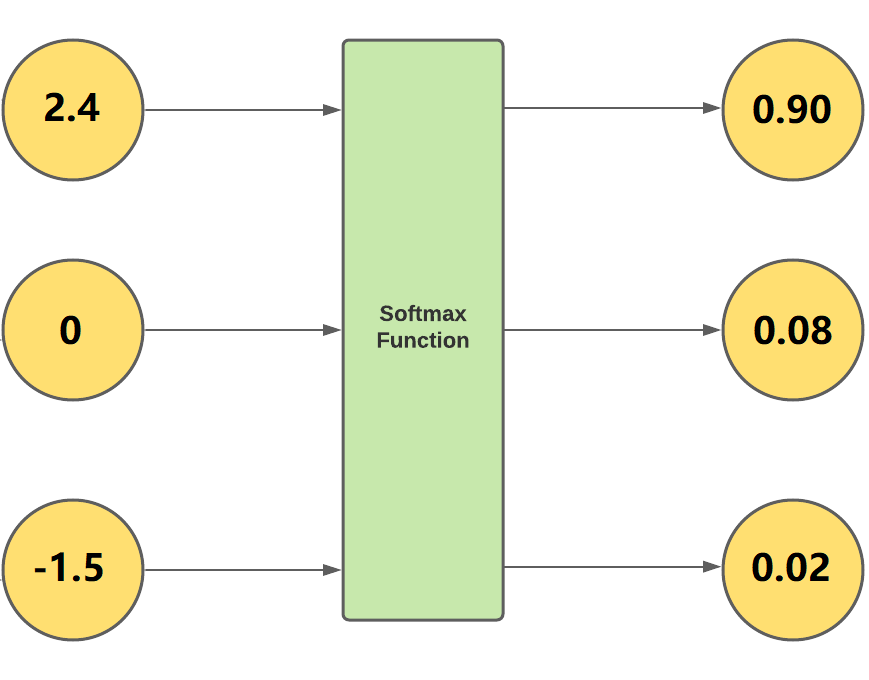
Below shows an example with $a=(2.4,0,-1.5)^T$ and $\boldsymbol{\sigma}(a)=(0.9001,0.0817,0.0182)^T.$

The mapping $\boldsymbol{\sigma}$ is soft in the sense that it is continuous in the input $a$. It is also max in the sense that it preserve the order of $a$:

$$a_{k}>a_j\quad \Leftrightarrow \quad \boldsymbol{\sigma}(a)_k>\boldsymbol{\sigma}(a)_j$$

The softmax function is surjective: for any posterior probabilities $f_1,\ldots,f_K$ satisfying the axioms of probability, there exists $a_1,\ldots,a_K$ satisfying the softmax representation. Nevertheless, such representation is not unique because it does not recognize a common shift in the input vector. That is, $$\boldsymbol{\sigma} \begin{pmatrix}a_{1}(x)\\\vdots\\a_{K}(x) \end{pmatrix} =\boldsymbol{\sigma} \begin{pmatrix}a_{1}(x)-c(x)\\\vdots\\a_{K}(x)-c(x) \end{pmatrix}$$ for any function $c(x):\mathcal{X}\rightarrow\mathbb{R}.$

To ensure one-to-one corresponding mappings between $f_k$'s and $a_k$'s, we shall set $a_K(x)\equiv 0$ unless specified otherwise.